Um adolescente vai a um parque de diversões

tendo, prioritariamente, o desejo de ir a um brinquedo

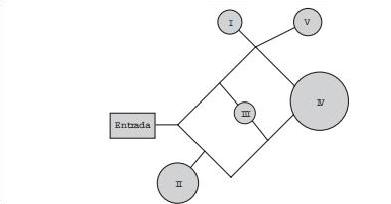
que se encontra na área IV, dentre as áreas I, II, III, IV

e V existentes. O esquema ilustra o mapa do parque,

com a localização da entrada, das cinco áreas com os

brinquedos disponíveis e dos possíveis caminhos para se

chegar a cada área. O adolescente não tem conhecimento

do mapa do parque e decide ir caminhando da entrada

até chegar à área IV.

Suponha que relativamente a cada ramificação

as opções existentes de percurso pelos caminhos

apresentem iguais probabilidades de escolha, que a

caminhada foi feita escolhendo ao acaso os caminhos

existentes e que, ao tomar um caminho que chegue a

uma área distinta da IV, o adolescente necessariamente

passa por ela ou retorna.

Nessas condições, a probabilidade de ele chegar à área

IV sem passar por outras áreas e sem retornar é igual a

Uma liga metálica sai do forno a uma temperatura de 3 000 °C e diminui 1% de sua temperatura a cada 30 min. Use 0,477 como aproximação para log₁₀(3) e 1,041 como aproximação para log₁₀(11).

O tempo decorrido, em hora, até que a liga atinja 30 °C é mais próximo de

O menor tempo possível, em hora, para conclusão da

construção da galeria, para atender às necessidades de

água do bairro, é de

Os alunos de uma escola utilizaram cadeiras iguais às

da figura para uma aula ao ar livre. A professora, ao final

da aula, solicitou que os alunos fechassem as cadeiras

para guardá-las. Depois de guardadas, os alunos fizeram

um esboço da vista lateral da cadeira fechada.

Qual é o esboço obtido pelos alunos?

Em um exame, foi feito o monitoramento dos níveis de

duas substâncias presentes (A e B) na corrente sanguínea

de uma pessoa, durante um período de 24 h, conforme

o resultado apresentado na figura. Um nutricionista, no

intuito de prescrever uma dieta para essa pessoa, analisou

os níveis dessas substâncias, determinando que, para

uma dieta semanal eficaz, deverá ser estabelecido um

parâmetro cujo valor será dado pelo número de vezes em

que os níveis de A e de B forem iguais, porém, maiores

que o nível mínimo da substância A durante o período de

duração da dieta.

Considere que o padrão apresentado no resultado

do exame, no período analisado, se repita para os dias

subsequentes.

O valor do parâmetro estabelecido pelo nutricionista, para

uma dieta semanal, será igual a

A bocha é um esporte jogado em canchas, que são terrenos planos e nivelados, limitados por tablados perimétricos de madeira. O objetivo desse esporte é lançar bochas, que são bolas feitas de um material sintético, de maneira a situá-las o mais perto possível do bolim, que é uma bola menor feita, preferencialmente, de aço, previamente lançada. A Figura 1 ilustra uma bocha e um bolim que foram jogados em uma cancha. Suponha que um jogador tenha lançado uma bocha, de raio 5 cm, que tenha ficado encostada no bolim, de raio 2 cm, conforme ilustra a Figura 2.

Considere o ponto C como o centro da bocha, e o ponto O como o centro do bolim. Sabe-se que A e B são os pontos em que a bocha e o bolim, respectivamente, tocam o chão da cancha, e que a distãncia entre A e B é igual a d. Nessas condições, qual a razão entre d e o raio do bolim?

Um vendedor de assinaturas de TV a cabo teve, nos 7 primeiros meses do ano, uma média mensal de 84 assinaturas vendidas. Devido a uma reestruturação da empresa, foi exigido que todos os vendedores tivessem, ao final do ano, uma média mensal de 99 assinaturas vendidas. Diante disso, o vendedor se viu forçado a aumentar sua média mensal de vendas nos 5 meses restantes do ano.

Qual deverá ser a média mensal de vendas do vendedor, nos próximos 5 meses, para que ele possa cumprir a exigência da sua empresa?

Uma caixa contém uma cédula de R$ 5,00, uma de R$ 20,00 e duas de R$ 50,00 de modelos diferentes. Retira-se aleatoriamente uma cédula dessa caixa, anota-se o seu valor e devolve-se a cédula à caixa. Em seguida, repete-se o procedimento anterior.

A probabilidade de que a soma dos valores anotados seja pelo menos igual a R$ 55,00 é

Um túnel deve ser lacrado com uma tampa de concreto.

A seção transversal do túnel e a tampa de concreto têm

contornos de um arco de parábola e mesmas dimensões.

Para determinar o custo da obra, um engenheiro deve

calcular a área sob o arco parabólico em questão. Usando

o eixo horizontal no nível do chão e o eixo de simetria da

parábola como eixo vertical, obteve a seguinte equação

para a parábola:

Qual é a área da parte frontal da tampa de concreto, em

metro quadrado?

Na figura estão representadas três retas no plano cartesiano, sendo P, Q e R os pontos de intersecções entre as retas, e A, B e C os pontos de intersecções dessas retas com o eixo x.

Essa figura é a representação gráfica de um sistema linear de três equações e duas incógnitas que